2D Chaotic Attractors

Clifford Attractor

The Clifford Attractor, created by Clifford Pickover, is a 4-parameter system. It is generated with plotting the attracting values through the two equations:

$x_{n+1} = sin(a*y_n) + c*cos(a*x_n)$ $y_{n+1} = sin(b*x_n) + d*cos(b*y_n)$

For the example at the left,

$a = -2, b = -2.4, c = 1.1, d = -0.9$

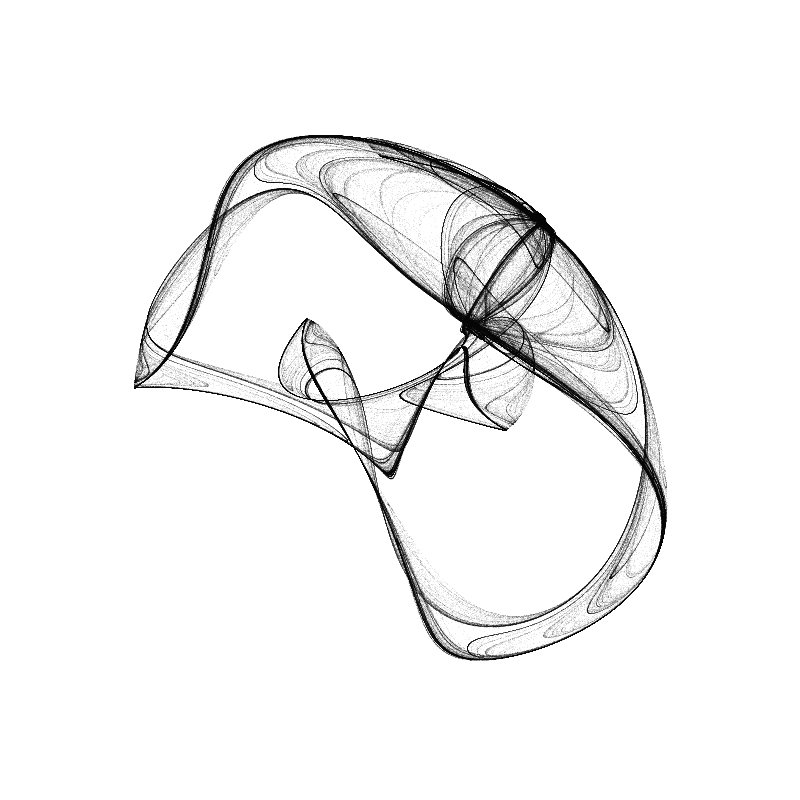
Peter de Jong attractor

The Peter de Jong attractor is a 4 parameter system. It is generated by plotting the attracting values of random initial points, using the equations:

$x_{n+1} = sin(a*y_n) - cos(b*x_n)$

$y_{n+1} = sin(c*x_n) - cos(d*y_n)$

In the case at the right,

$a = 0.970, b = -1.899, c = 1.381, d = -1.506$

Duffing Attractor

The Duffing Attractor is a 3-parameter system that draws a trajectory from an initial point (0, 0). The equations to generate it are:

$\frac{dx}{dt} = y$

$\frac{dy}{dt} = x - x^3 - a*y + b*cos(w*t)$

Which is a product of the differential equation:

$\ddot x + \delta*\dot x + \alpha*x + \beta*x^3 = \gamma*\cos(\omega*t)$

At the left,

$a = 0.35, b = 0.3, w = 1$

Ikeda Attractor

The Ikeda Attractor was created by Kensuke Ikeda, Hiroaki Daido, and O. Akimoto to generalize a map of light travelling through a ring cavity containing a non-linear dielectric medium (NLDM). It is generated in the complex plane using the sequence:

$z_{n+1} = A + B*z_n*e^{\frac{i*K}{|z_n|^2+1} + C}$

$A$ and $C$ are parameters for outside light, $B$ is for dissipation, and $K$ is the saturation effect of the NLDM. A simplified and real version of the above sequence is:

$t_n = 0.4 - \frac{6}{1 + x_n^2 + y_n^2}$

$x_{n+1} = 1 + u*(x_n*cos(t_n) - y_n*sin(t_n))$

$y_{n+1} = u*(x_n*sin(t_n) + y_n*cos(t_n))$

When $u \ge 0.6$ , the result is a chaotic attractor.

At the right, $u = 0.9$

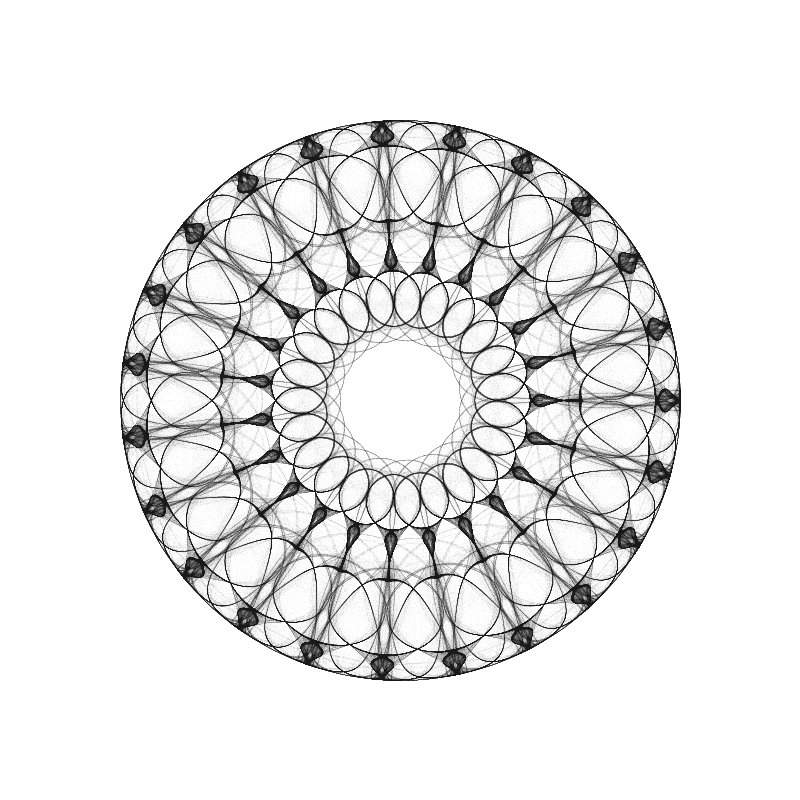
Symmetric Icon Attractor

Created by Michael Field and Martin Golubitsky, the Symmetric Icon Attractor is a 6-parameter system. It is generating by plotting every iteration on a point ( $x_0$ , $y_0$ ) which is initialized at (0.01, 0.01). The equations to generate it are made by defined by code:

In the case at the left,

$l = 2.409, a = -2.5, b = 0, g = 0.9, o = 0, d = 23$

Tinkerbell Attractor

The Tinkerbell Attractor is likely named for the character Tinker Bell. It is a 4-parameter system, and it is generated by plotting every iteration ( $x_n$ , $y_n$ ). The equations to generate the Tinkerbell Attractor are:

$x_{n+1} = x_n^2 - y_n^2 + a*x_n + b*y_n$

$y_{n+1} = 2*x_n*y_n + c*x_n + d*y_n$

In the image at the right,

$x_0 = -0.72, y_0 = -0.64$

$a = 0.9, b = -0.6013, c = 2, d = 0.5$

Johnny Svensson Attractor

The Johnny Svensson Attractor (created by Johnny Svensson) is a twist on the Peter de Jong attractor. It has 4 parameters, and is generated by taking lots of random initial points and putting them through the equation until they go to a value, which is then plotted. The equations to generate the attractor are:

$x_{n+1} = d*sin(a*x_n) - sin(b*y_n)$

$y_{n+1} = c*cos(a*x_n) + cos(b*y_n)$

At the left,

$a = c = 1.4, b = 1.56, d = -6.56$

Gumowski-Mira Attractor

The Gumowski-Mira Attractor is a 2-parameter system. It is generated by plotting many iterations of many initial points through these equations:

$f(x) = a*x + 2*(1-a)*x^2*(1 + x^2)^{-2}$

$x_{n+1} = b*y_n + f(x_n)$

$y_{n+1} = f(x_{n+1}) - x_n$

At the right,

$a = -0.192, b = 0.982$

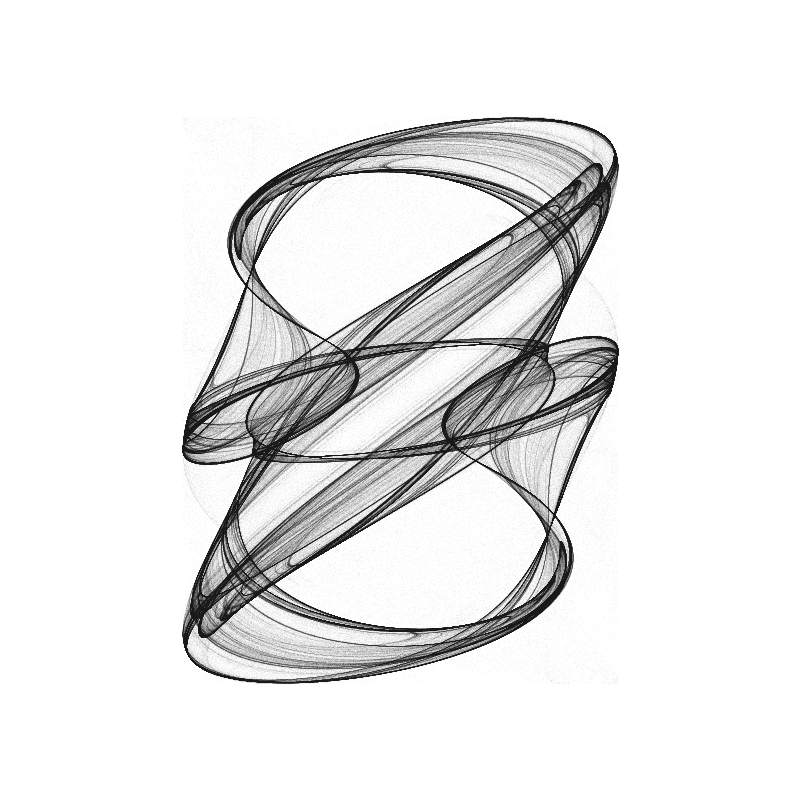
Fractal Dreams (SSSS)

Coming from Clifford Pickover’s book “Chaos in Wonderland”, all modes of the Fractal Dreams Attractor require 4 parameters. It is generated by plotting the many iterations of many initial points. In the SSSS version, the equations are:

$x_{n+1} = \sin(y*b) + c*\sin(x*b)$

$y_{n+1} = \sin(x*a) + d*\sin(y*a)$

At the left,

$a = 1.468, b = 2.407, c = 0.194, d = 1.438$

Quadratic Strange Attractor

The Quadratic Chaotic Attractor, described by Clint Sprott is a 12-parameter system. Its parameters are described by a letter code with letters A-Y. Each of these represent a value between -1.2 and 1.2, with $A = -1.2$ and every other letter being incremented by 0.1 above the previous letter. This number code is converted into the coefficients $a_0$ through $a_{11}$ , with each letter in the code matching each coefficient when converted to their number value. The equations to generate it are:

$x_{n+1} = a_0 + a_1*x_n + a_2*x_n^2 + a_3*$
$x_n*y_n + a_4*y_n + a_5*y_n^2$

$y_{n+1} = a_6 + a_7*x_n + a_8*x_n^2 + a_9*$
$x_n*y_n + a_{10}*y_n + a_{11}*y_n^2$

At the right, the code is:

$CVQKGHQTPHTE$

Cubic Strange Attractor

Created by Clint Sprott, the Cubic Strange Attractor is the phase-space of a 20-parameter system. It works in a similar fashion to the Quadratic Strange Attractor, in which a 20 letter code is created (one for each parameter), and each letter is a letter A-Y. Then, let $A = -1.2$ and $Y = 1.2$ , and every letter in between is 0.1 above the previous letter, for example $B = -1.1, C = -1...$ These number values correlate to each of the constants. The equations to generate the attractor are:

$x_{n+1} = a_0 + a_1*x_n + a_2*x_n^2 + a_3*x_n^3 +$
$a_4*x_n^2*y_n + a_5*x_n*y_n + a_6*x_n*y_n^2 +$
$a_7*y_n + a_8*y_n^2 + a_9*y_n^3$

$y_{n+1} = a_{10} + a_{11}*x_n + a_{12}*x_n^2 + a_{13}*x_n^3 +$
$a_{14}*x_n^2*y_n + a_{15}*x_n*y_n + a_{16}*x_n*y_n^2 +$
$a_{17}*y_n + a_{18}*y_n^2 + a_{19}*y_n^3$

At the left the code is:

$ISMHQCHPDFKFBKEALIFD$

Quartic Strange Attractor

The Quartic Strange Attractor, from Clint Sprott, is the phase-space or Attractor of a 30 parameter system ( $a_0$ to $a_{29}$ ). The parameters are based on a 30-letter code (with a one-to-one correspondence). In this code, the letters are only A-Y. These all represent a number between -1.2 and 1.2, with increments of 0.1 (eg. $A = -1.2, B = -1.1,..., Y = 1.2$ .) The parameters are equal to its letter’s numerical value. The equations to generate it are:

$x_{n+1} = a_0 + a_1*x_n + a_2*x_n^2 + a_3*x_n^3 +$
$a_4*x_n^4 + a_5*x_n^3*y_n + a_6*x_n^2*y_n +$
$a_7*x_n^2*y_n^2 + a_8*x_n*y_n + a_9*x_n*y_n^2 +$
$a_{10}*x_n*y_n^3 + a_{11}*y_n + a_{12}*y_n^2 +$
$a_{13}*y_n^3 + a_{14}*y_n^4$

$y_{n+1} = a_{15} + a_{16}*x_n + a_{17}*x_n^2 + a_{18}*x_n^3 +$
$a_{19}*x_n^4 + a_{20}*x_n^3*y_n + a_{21}*x_n^2*y_n +$
$a_{22}*x_n^2*y_n^2 + a_{23}*x_n*y_n + a_{24}*x_n*y_n^2 +$
$a_{25}*x_n*y_n^3 + a_{26}*y_n + a_{27}*y_n^2 +$
$a_{28}*y_n^3 + a_{29}*y_n^4$

At the right, the code is:

$FUXRRRUIRDYKDUB-$
$PHHOMOBRIRBINCS$

Quintic Strange Attractor

Based on works of Clint Sprott, the Quintic Strange Attractor is the phase-space/basin of attraction of a 42-parameter system. The 42 parameters ( $a_0-a_{41}$ ) are determined by a 42 letter code, one letter per parameter. The letters in that code are strictly A-Y. The letters have numerical values, between -1.2 and 1.2 in increments of 0.1. $A = -1.2, B = -1.1,..., Y = 1.2$ . The parameters take on these numerical values from their letter. The equations to generate it are:

$x_{n+1} = a_0 + a_1*x_n + a_2*x_n^2 + a_3*x_n^3 +$
$a_4*x_n^4 + a_5*x_n^5 + a_6*x_n^4*y_n + a_7*x_n^3*y_n +$
$a_8*x_n^3*y_n^2 + a_9*x_n^2*y_n + a_{10}*x_n^2*y_n^2 +$
$a_{11}*x_n^2*y_n^3 + a_{12}*x_n*y_n + a_{13}*x_n*y_n^2 +$
$a_{14}*x_n*y_n^3 + a_{15}*x_n*y_n^4 + a_{16}*y_n$
$a_{17}*y_n^2 + a_{18}*y_n^3 + a_{19}*y_n^4 + a_{20}*y_n^5$

$y_{n+1} = a_{21} + a_{22}*x_n + a_{23}*x_n^2 + a_{24}*x_n^3 +$
$a_{25}*x_n^4 + a_{26}*x_n^5 + a_{27}*x_n^4*y_n + a_{28}*x_n^3*y_n +$
$a_{29}*x_n^3*y_n^2 + a_{30}*x_n^2*y_n + a_{31}*x_n^2*y_n^2 +$
$a_{32}*x_n^2*y_n^3 + a_{33}*x_n*y_n + a_{34}*x_n*y_n^2 +$
$a_{35}*x_n*y_n^3 + a_{36}*x_n*y_n^4 + a_{37}*y_n$
$a_{38}*y_n^2 + a_{39}*y_n^3 + a_{40}*y_n^4 + a_{41}*y_n^5$

At the left the code is:

$GEQGOYIKQQPEUJBKPXTVU-$
$SJHOVJDUAYYPRNTXFLGAM$

Sextic Strange Attractor

Based on ideas by Clint Sprott, the Sextic Chaotic Attractor is the phase-space/basin of attraction of a 56-parameter system. The parameters are dependent on a code, with 56 letters, one for each parameter. The letters have a numerical value in which the parameter takes on. The letters are A to Y, and their numbers are -1.2 to 1.2, being incremented by 0.1. The equations to generate it are:

$x_{n+1} = a_0 + a_1*x_n + a_2*x_n^2 + a_3*x_n^3 +$
$a_4*x_n^4 + a_5*x_n^5 + a_6*x_n^6 + a_7*x_n^5*y_n +$
$a_8*x_n^4*y_n + a_9*x_n^4*y_n^2 + a_{10}*x_n^3*y_n +$
$a_{11}*x_n^3*y_n^2 + a_{12}*x_n^3*y_n^3 + a_{13}*x_n^2*y_n +$
$a_{14}*x_n^2*y_n^2 + a_{15}*x_n^2*y_n^3 + a_{16}*x_n^2*y_n^4 +$
$a_{17}*x_n*y_n + a_{18}*x_n*y_n^2 + a_{19}*x_n*y_n^3 +$
$a_{20}*x_n*y_n^4 + a_{21}*x_n*y_n^5 + a_{22}*y_n +$
$a_{23}*y_n^2 + a_{24}*y_n^3 + a_{25}*y_n^4 + a_{26}*y_n^5 +$
$a_{27}*y_n^6$

$y_{n+1} = a_{28} + a_{29}*x_n + a_{30}*x_n^2 + a_{31}*x_n^3 +$
$a_{32}*x_n^4 + a_{33}*x_n^5 + a_{34}*x_n^6 + a_{35}*x_n^5*y_n +$
$a_{36}*x_n^4*y_n + a_{37}*x_n^4*y_n^2 + a_{38}*x_n^3*y_n +$
$a_{39}*x_n^3*y_n^2 + a_{40}*x_n^3*y_n^3 + a_{41}*x_n^2*y_n +$
$a_{42}*x_n^2*y_n^2 + a_{43}*x_n^2*y_n^3 + a_{44}*x_n^2*y_n^4 +$
$a_{45}*x_n*y_n + a_{46}*x_n*y_n^2 + a_{47}*x_n*y_n^3 +$
$a_{48}*x_n*y_n^4 + a_{49}*x_n*y_n^5 + a_{50}*y_n +$
$a_{51}*y_n^2 + a_{52}*y_n^3 + a_{53}*y_n^4 + a_{54}*y_n^5 +$
$a_{55}*y_n^6$

At the right the code is:

$VDKHXMRTJAHALL-$
$RVTVNYMDMCDHOG-$
$NLJOPTJUNXDLCF-$
$NOUOCWMVAIQKSS$

Hénon Map Bifurcation

For the Hénon Map, the image at the right is generated by plotting “attractor” values as a parameter (x-axis) increases. These “attractor” values are values that any input tends to go towards after many iterations of the mapping equation.

The Hénon Map is given by the equations:

$|^{x_{n+1}=1-ax_n^2+y_n}_{y_{n+1}=bx_n}$

The Sequelaen Collection

Art in Math

2D Chaotic Attractors

Leave a comment Cancel reply

Share this:

Leave a comment Cancel reply