Equations

y = ?(x)

The function is known as Minkowski’s Question Mark Function (named for Hermann Minkowski). It maps irrational numbers to rational numbers and has fractal properties, it is defined as:

$?(x) = a_0 + 2*\displaystyle\sum_{n=1}^\infty \frac{(-1)^{n+1}}{2^{a_1+...+a_n}}$

Or:

$?(x) = a_0 + 2*\displaystyle\sum_{n=1}^\infty \frac{(-1)^{n+1}}{\displaystyle\prod_{j=1}^n 2^{a_j}}$

Where $a_n$ is the $n^{th}$ term of the continued fraction of $x$ (only works for irrational $x$ )

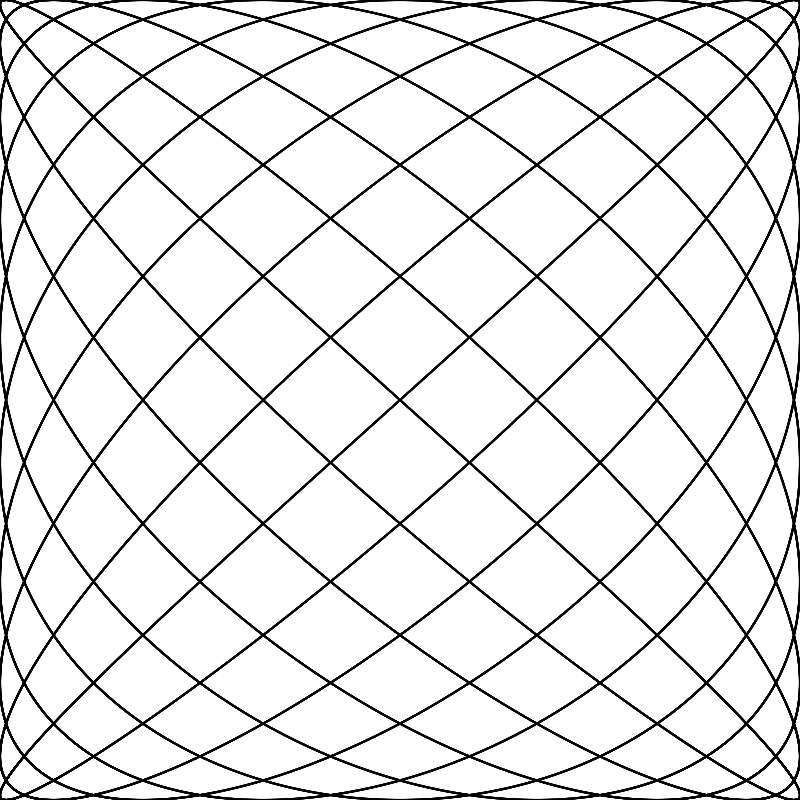
Lissajous Curves

Lissajous Curves or Bowditch Curves, named for Jules Lissajous and Nathaniel Bowditch. It is a parametric system and is generated through the equations:

$x = A*\sin(a*t + \delta)$

$y = B*\sin(b*t)$

$2*A$ and $2*B$ are the width and height of the final product, respectively. Higher $a$ and $b$ increase complexity, however Lissajous curves with ratios equivalent to smaller ratios, they are the same. For example, $a = 1, b = 2$ and $a = 2, b = 4$ produce the same curve, as $\frac{1}{2} = \frac{2}{4}$ .